티스토리 뷰

초과 미만 뜻 이상 이하 반대말 자료집
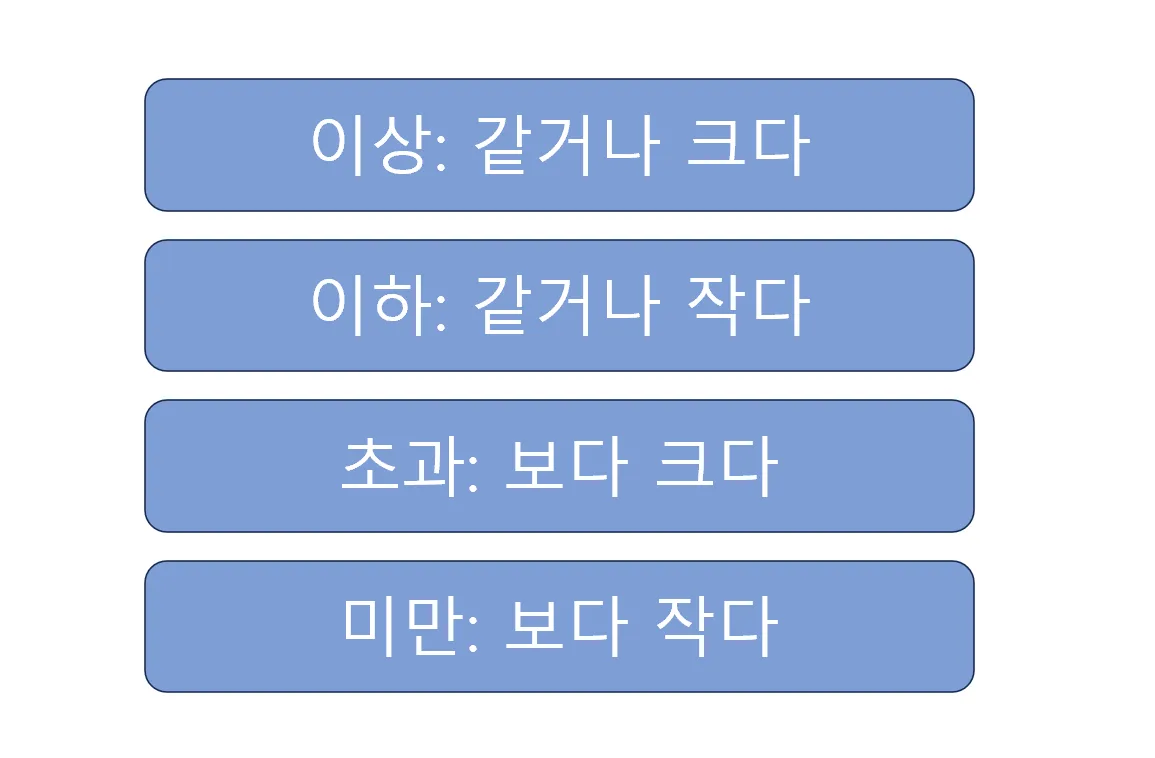
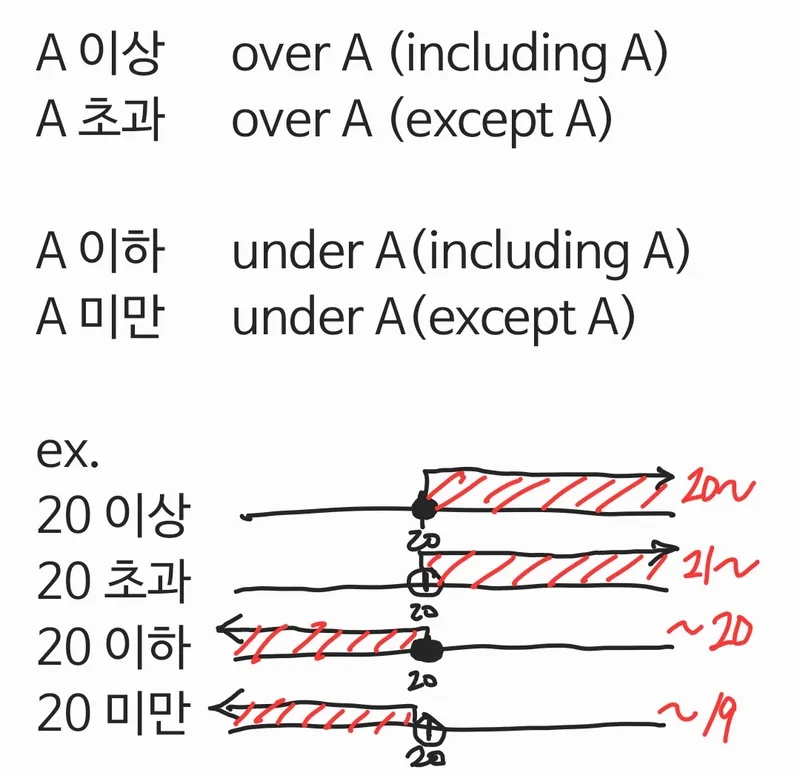
초과 미만 뜻과 이상 이하는 수학에서 가장 헷갈리는 개념 중 하나로, 초과는 '그 수보다 큰', 미만은 '그 수보다 작은', 이상은 '그 수보다 크거나 같은', 이하는 '그 수보다 작거나 같은'을 의미합니다.
수의 대소관계를 나타내는 기본 용어들
초과 미만 뜻 이상 이하 반대말 자료집에 대해 궁금하신 분들은 아래를 참고하세요!




수학에서 사용하는 초과 미만 뜻을 제대로 파악하려면 먼저 이 용어들이 어떤 맥락에서 나왔는지 알아야 해요. 사실 많은 학생들이 이 개념을 단순 암기로만 접근하는데, 그러면 나중에 복잡한 문제에서 실수하기 쉽거든요.


제가 중학교 때 처음 이 개념을 배울 때도 정말 헷갈렸어요. 특히 '초과'라는 단어가 '넘어선다'는 뜻인데, 그 기준점이 포함되는지 안 되는지가 가장 애매했죠. 근데 한번 정확히 이해하고 나니까 오히려 다른 수학 개념들보다 훨씬 명확하더라고요.
초과와 미만의 핵심 개념
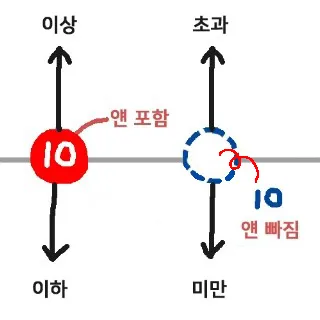
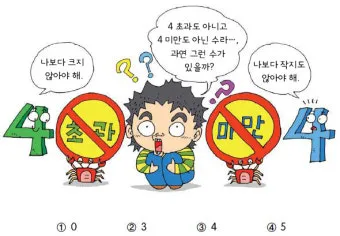
초과(超過)는 말 그대로 '넘어선다'는 뜻입니다. 어떤 기준점을 완전히 넘어서는 것을 의미해요. 예를 들어 '10 초과'라고 하면 10보다 큰 수들, 즉 10.1, 11, 15, 100 같은 숫자들이 해당되죠. 여기서 중요한 건 기준점인 10은 절대 포함되지 않는다는 거예요.
반대로 미만(未滿)은 '아직 차지 않았다'는 의미입니다. 어떤 기준점에 도달하지 못한 상태를 나타내요. '10 미만'이면 10보다 작은 수들, 즉 9.9, 5, -2 같은 숫자들이 포함되고, 마찬가지로 기준점 10은 포함되지 않아요.



이걸 좀 더 직관적으로 이해하려면 수학 개념 정리 자료를 참고해보세요. 시각적인 자료로 보면 훨씬 쉽게 와닿을 거예요.
실제로 초과 미만 뜻을 정확히 알고 있으면 여러 시험에서 엄청 도움이 돼요. 특히 확률과 통계, 함수 문제에서 정의역과 치역을 구할 때 자주 나오거든요.
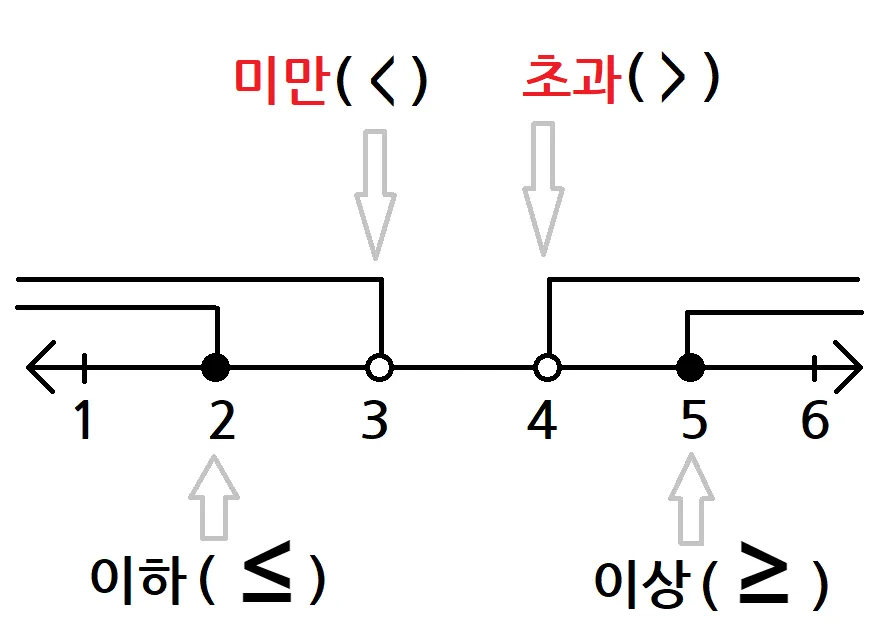
부등호 기호로 표현하는 방법
수학에서는 초과와 미만을 부등호로 표현합니다. 이 부분이 생각보다 중요해요. 많은 학생들이 기호만 외우고 끝내는데, 실제로는 문장으로 된 조건을 기호로 바꾸는 연습을 많이 해야 돼요.


x > a는 'x가 a보다 크다' 즉 'x는 a 초과'를 의미합니다. 여기서 a는 포함되지 않아요. 반대로 x < a는 'x가 a보다 작다' 즉 'x는 a 미만'을 뜻하죠.
부등호의 방향을 기억하는 꿀팁이 하나 있어요. '>'는 입이 더 큰 쪽(왼쪽)이 더 큰 수라고 생각하면 됩니다. 그러면 절대 헷갈리지 않아요. 제가 학창시절에 써먹었던 방법인데 정말 효과적이에요!
포함 관계를 나타내는 이상과 이하



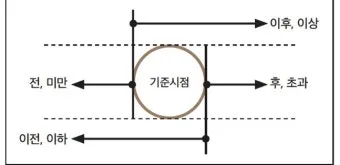
초과 미만과 달리 이상 이하는 기준점을 포함한다는 게 가장 큰 특징이에요. 이 부분을 정확히 이해하면 반대말 관계도 자연스럽게 파악할 수 있어요.


실생활에서 이상 이하를 가장 많이 접하는 곳이 바로 나이 제한이나 자격 조건들이에요. '만 18세 이상'이라고 하면 18세도 포함되잖아요. 이런 식으로 생각하면 훨씬 쉬워져요.
이상과 이하의 완벽 구분법
이상(以上)은 '그것부터 위로'라는 뜻입니다. 기준점을 포함해서 그보다 큰 모든 수를 의미해요. '10 이상'이면 10, 10.1, 11, 100 등이 모두 해당되죠. 기준점인 10이 포함된다는 게 초과와의 결정적 차이점이에요.
이하(以下)는 '그것부터 아래로'를 뜻합니다. 기준점을 포함해서 그보다 작은 모든 수가 포함돼요. '10 이하'라면 10, 9.9, 5, -10 등이 해당되고요.



제가 개인적으로 학생들을 가르쳐보니까, 이상 이하는 상대적으로 이해하기 쉬워해요. 왜냐하면 일상생활에서 자주 접하는 표현이거든요. 하지만 초과 미만은 좀 어려워하더라고요.
부등호로 표현하면 x ≥ a가 'x는 a 이상', x ≤ a가 'x는 a 이하'입니다. 등호(=)가 포함된 기호라는 게 핵심이에요.
생활 속 다양한 적용 사례

초과 미만 뜻과 이상 이하 반대말을 실생활에서 어떻게 활용하는지 알아보면 개념이 더 확실해져요. 생각보다 우리 주변에 이런 표현들이 정말 많거든요.



먼저 쇼핑몰에서 자주 보는 '30,000원 이상 무료배송'을 생각해보세요. 이건 30,000원도 포함해서 그보다 높은 금액에 대해 무료배송을 해준다는 뜻이에요. 만약 '30,000원 초과 무료배송'이라고 했다면 30,001원부터 무료배송이 되는 거죠.
놀이기구 이용 제한도 좋은 예시예요. '키 120cm 이상'이라고 하면 120cm인 아이도 탈 수 있어요. 하지만 '키 120cm 초과'라고 했다면 120cm는 안 되고 121cm부터 가능한 거죠.
성적 등급도 마찬가지예요. 'A등급 90점 이상'이면 90점도 A등급이에요. '90점 초과'였다면 91점부터 A등급인 거고요. 이런 차이를 정확히 아는 게 중요해요.

온도 조건도 흥미로운 사례인데요. '영상 5도 이상에서 사용 가능'이라고 하면 정확히 5도에서도 사용할 수 있어요. 하지만 '5도 초과'라고 하면 5.1도부터 사용 가능한 거죠.
실수하지 않는 완벽 학습법

지금까지 초과 미만 이상 이하의 개념을 살펴봤는데, 이제 이걸 확실하게 내 것으로 만드는 방법을 알아볼게요. 단순히 개념만 아는 것과 실제 문제에서 정확히 적용하는 건 완전히 다른 차원이거든요.
제가 수년간 학생들을 지도하면서 발견한 가장 효과적인 학습법들을 정리해봤어요. 이 방법들을 차근차근 따라하면 더 이상 헷갈릴 일이 없을 거예요.


절대 틀리지 않는 암기 꿀팁
가장 확실한 방법은 언어적 의미를 활용한 암기법이에요. 한자 뜻을 이용하면 정말 쉬워져요.
초과(超過)의 '초(超)'는 '뛰어넘다'는 뜻이에요. 완전히 뛰어넘는 거니까 기준점은 포함하지 않죠. 미만(未滿)의 '미(未)'는 '아직 아니다', '만(滿)'은 '차다'라는 뜻이에요. 아직 차지 않았으니까 기준점 미포함인 거죠.
이상(以上)의 '이(以)'는 '~부터'라는 뜻이에요. 그 지점부터 시작하니까 포함되는 거고요. 이하(以下)도 마찬가지로 그 지점까지 포함한다는 의미예요.


또 다른 암기법으로는 영어를 활용하는 방법도 있어요. 초과는 'more than', 미만은 'less than'으로 than 앞에는 등호가 없어요. 이상은 'greater than or equal to', 이하는 'less than or equal to'로 'equal to'가 들어가죠.
저는 개인적으로 숫자선을 그려서 암기하는 방법도 추천해요. 0부터 10까지 숫자선을 그리고 5를 기준으로 각 개념을 표시해보세요. 시각적으로 보면 훨씬 오래 기억돼요.
실전 문제로 완벽 마스터하기
이론을 아는 것과 실제 문제를 푸는 것은 다른 영역이에요. 특히 조건이 여러 개 겹치거나 복합적인 상황에서는 더욱 신중해야 해요.
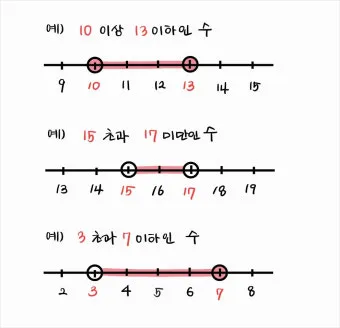
예를 들어 '5 초과 10 미만'이라는 조건이 나오면 어떻게 해석해야 할까요? 5는 포함되지 않고 10도 포함되지 않으니까 5 < x < 10이 되는 거예요. 실수로 5나 10을 포함시키면 안 되죠.
'3 이상 7 이하'는 3 ≤ x ≤ 7로 양쪽 끝점이 모두 포함돼요. 이런 차이를 정확히 구분하는 게 중요해요.
복잡한 조건 문제를 풀 때는 먼저 각 조건을 부등호로 바꾸는 연습부터 해야 해요. 그 다음에 합집합이나 교집합을 구하면 되거든요. 순서를 바꿔서 접근하면 실수하기 쉬워요.
초과 미만 뜻 이상 이하 반대말 자료집에 대해 더 알고싶은 내용은 아래를 확인하세요!

확률과 통계에서도 마찬가지예요. 연속확률변수의 확률을 구할 때 P(X > a)와 P(X ≥ a)는 연속분포에서는 같지만, 이산분포에서는 다르죠. 이런 세부적인 차이까지 알고 있어야 완벽해요.
제가 학생들한테 항상 강조하는 건 문제를 읽을 때 조건들을 정확히 파악하는 습관을 기르라는 거예요. 특히 '~보다 크다', '~보다 작거나 같다' 같은 표현이 나오면 바로 부등호로 바꿔서 써보는 연습을 하세요.



그리고 답을 구한 다음에는 반드시 검산을 해보세요. 경계값을 대입해서 조건에 맞는지 확인하는 거죠. 이 과정에서 실수를 많이 발견할 수 있어요.
초과 미만 뜻 이상 이하 반대말 자료집에 대한 보다 자세한 내용은 아래 내용을 확인해보세요!

결론적으로 초과 미만 뜻과 이상 이하 반대말을 완벽하게 이해하려면 개념 암기와 실전 연습을 병행해야 해요. 특히 일상생활 속 사례들을 자주 떠올려보면서 자연스럽게 체화시키는 게 중요하죠. 이 글에서 정리한 내용들을 바탕으로 꾸준히 연습하면 분명히 마스터할 수 있을 거예요!
수학은 암기과목이 아니라 이해과목이에요. 단순히 외우기보다는 왜 그런지, 어떤 맥락에서 사용되는지를 파악하는 게 훨씬 효과적이에요. 초과 미만 이상 이하도 마찬가지로 각각의 의미와 쓰임새를 정확히 이해하면 절대 헷갈리지 않을 거예요.
앞으로 이런 개념들을 접할 때마다 이 글의 내용을 떠올려보세요. 그러면 어떤 상황에서도 자신있게 문제를 해결할 수 있을 거예요. 수학 실력 향상에 조금이라도 도움이 되었으면 좋겠어요!
볼만한 글



